Calorimetry and Molar Enthalpy
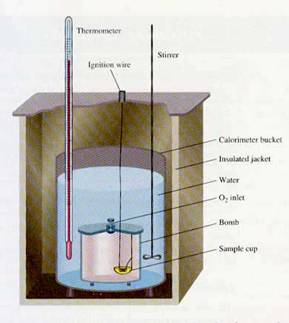
The purpose of calorimetry is to use an instrument known as a calorimeter to determine the enthalpy of a substance undergoing chemical change. In a calorimeter known as a bomb calorimeter, it is the enthalpy of combustion that is measured. This is how the caloric content of foods is determined. In both cases, since the heat absorbed or released is proportional to the amount of reactant used, molar enthalpy = DH/n is a more meaningful and characteristic quantity.
In a bomb calorimeter, the actual chamber holding the sample is known as a “bomb”. After opening its lid, we place a weighed sample in a cup at the bottom of the bomb. It is sealed, and through a valve, O2 is delivered, saturating the bomb to prepare it for ignition. The bomb is then secured within a calorimeter bucket that is filled with water (the water is the environment which will absorb the heat of combustion). A stirrer keeps the temperature of the water evenly distributed. A thermometer allows us to measure the initial temperature; the ignition wire connected to a high voltage source initiates the explosion; heat is released, and we measure the maximum temperature attained.
Q = mc DT
m = mass of the water in the calorimeter in grams (because of c ‘s units; see below), or the mass of whatever substance is acting as the environment. In reality we should assume that the material part of the calorimeter also absorbs heat. But in this course, we usually ignore that part.
c = specific heat of water or whatever is acting as the environment.
Note c is usually expressed in ![]() ,
so that Q is in Joules
,
so that Q is in Joules
DT = Tf – Ti.
To get DH, remember:
DH = - Q.
We convert J to kJ by /1000, and then
Molar enthalpy = DH/n. n = number of moles of reactant. So we convert the carefully measured mass in to moles by dividing by molar mass.
In molar heat of neutralization problems, n = CV, where
C = concentration in “M” = moles/L.
V = volume in litres.
In-Class Examples
1. 9.0
grams of charcoal (C) were completely consumed in a bomb calorimeter. If we
assume that the 2.0 L of water absorbed all of the heat released by the
charcoal, and if the temperature of the water increased from 20.25 to 56.04oC,
what is the molar enthalpy of carbon?
Q = mc DT
= 2000g(4.19
J/(g C))(56.04-20.25)
Notice that we do not include the 9 g. We only use the mass of the environment absorbingthe heat.
= 299 920 J
DH = - Q
= - 299 920 J = -299.92 kJ
n = 9.0g / 12.01 g/mole = 0.7493 mole
DH/n = -299.92 kJ/ 0.7493 mole = -400.27kJ/mole of C = - 4.0 X 102 kJ/mole( sig figs)
2. CS2, a very flammable liquid, has a molar enthalpy of -1028 kJ/mole. What do you expect aluminum's final temperature to be if 1.0 kg of Al is initially at 20.0 C, and it absorbs all the heat from the following sample of CS2:
mass of CS2 before burning: 22.6 g
mass of CS2 after burning: 11.6 g
specific heat capacity of Al: 0.900 J/[g C]
mass
= 22.6 - 11.6 = 11.0 g
11.0g/ 76g/mole = 0.1447 moles
n(DH/n) = DH =
0.1447moles (-1028
kJ/mole) = -148.79 kJ = --148 790 J
Q = - DH =
148790 J
Q = mc DT
148790 J = 1000g(0.900)(Tf - 20)
Tf = 185.3 C = 1.9 X 102 0C
3. 300 mL of 0.2 M aqueous KOH neutralizes 150 mL of aqueous 0.2 M H2SO4. We go from an average initial temperature of 22.3 oC to a maximum of 29.2 C. Calculate the molar heat(enthalpy) of neutralization of KOH.
2KOH + H2SO4 à K2SO4
+ 2 H2O
Q = mc DT
= (300 + 150 g)(4.19)(29.2-22.3)
We use all aqueous volumes which with a density of 1.0g/ml will have a mass of 300 and 150, respectively. 300 ml of KOH(aq), people forget , has 300ml of water arounf the K+ and OH- ions. Same with the acid.
=13009.95 J
DH = - Q
= - 13009.95 J = -13.01 kJ
n = CV = 0.2mole/L(0.300 L) = 0.06
moles
DH/n =
-13.10 kJ/0.06 moles = -217 kJ/mole of KOH = -2 X 102 kJ/mole of KOH
Very important: When plugging in V, make sure by looking at the stoichiometry that you consider only the volume of the KOH
(since they asked for its enthalpy)that actually
reacted. If they had used an excess of KOH like 600 ml, this would have changed
the value for m but not for V. How do you calculate the amount in L of KOH that
actually reacts with a given amount of acid?
(0.2 moles/L H2SO4) (0.150
L) (2 moles KOH/ 1 mole H2SO4)(L/0.2 moles KOH) = 0.300 L
Basically VB = volume of the base= [CAVA/CB]
[nB/nA] where nB = moles of base or
VA = [CBVB/CA] [nA/nB]
4. Find the final temperature of the following mixture:
400. g of Cu initially at 99.0 oC
25 L of water initially at 10.0 oC
c for Cu = 0.39 J/[g C]
QH2O = - QCu ( because the heat lost by Cu will be gained by the water)
mH2OcH2O (Tf - TH2O) = -mCucCu (Tf - TCu); Note that they reach the same final temperature.
25000g (4.19)( Tf-10) = -400 ( 0.39)( Tf -99)
Tf = 10.1 C = 10. oC
The temperature change is insignificant ( especially if we pay attention to significant figures) because the amount of water is much greater than the amount of Cu, and because water has a higher specific heat than Cu.