Module 3 Rates
of Chemical Reactions
1. What is the rate of
a reaction?
Solution:
The rate of a reaction is
the amount of reactant that disappears or product that appears per unit time.
Mathematically it is the ratio of the change in the amount of a substance to
the change in time.
![]()
Example 1 Mg(s) + 2 HCl(aq) à MgCl2(aq) + H2![]()
a. A student places a piece of magnesium in acid and measures
0.12 moles of hydrogen gas after 2.0 minutes. Six minutes after having added
the Mg, a total of 0.36 moles of hydrogen were collected. Find the average rate
of production of hydrogen gas between 2.0 and 6.0 minutes.
Solution:
Rate = DH2/ Dt = [0.36- 0.12] / [6.0-2.0] = 0.060 moles
of H2/minute
b. Find the average rate of disappearance of hydrochloric acid
between 2.0 and 6.0 minutes.
Solution:
If we examine the
ratio of HCl/ H2 in the balanced equation
we notice that it is 2/1. So the rate of disappearance of HCl
will be twice the rate of hydrogen production.
Answer: -0.060
moles of H2/minute [2 moles of HCl/ mole
of H2] = -0.12 mole HCl/minute. The
negative indicates that the reactant is being used up.
Example 2 A student places 5.0
moles of hydrogen and 5.0 moles of iodine into a 2.0 L container and measures
the amount of HI formed according to:
H2(g) + I2(g) à 2 HI (g)
Here’s her data:
|
Time (minutes) |
0.0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
|
Moles of HI present |
0.0 |
4.0 |
6.0 |
7.4 |
8.4 |
9.0 |
9.2 |
Graph the amount of leftover
H2 versus time (for the first 6.0 minutes)and
find the average rate of hydrogen consumed.
Solution:
|
Time (minutes) |
0.0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
|
Moles of HI
present |
0.0 |
4.0 |
6.0 |
7.4 |
8.4 |
9.0 |
9.2 |
|
Moles of hydrogen that reacted |
=HI/2= 0 |
=HI/2= 4.0/2.0=2.0 |
3.0 |
3.7 |
4.2 |
4.5 |
4.6 |
|
Moles of
hydrogen left over |
Initially there
were 5.0 moles (see question),
so now we have 5.0 –0 = 5.0 moles |
5.0-2.0=3.0 |
2.0 |
1.3 |
0.8 |
0.5 |
0.4 |
We use the third
row to obtain the rate:
Rate =
[4.6-0]/[6.0-0]=0.77 moles of hydrogen/minute.
But to graph we
need the last row of data since we are being asked for leftover
hydrogen.
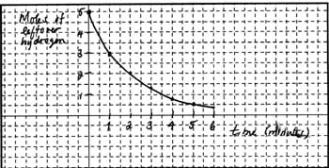
Notice that since the points on
the graph generate a curve, the rate at which hydrogen disappears
keeps changing. That's why we refer to the rate we calculated as an average
rate. To get the instantaneous rate (the rate at any given instant) we would
have to draw a tangent line to the curve at that given moment, and obtain the
slope of the tangent line. If you imagine successive tangent lines drawn to the
curve from left to right, the slopes of the tangents become progressively more gentle. In other words, the rate at which hydrogen disappears keeps decreasing with time.